Eテレ（NHK教育）で深夜にやっている5分番組「2355」で、算数パズル（?）をやっていたのでご紹介。

三角形の内角の和が180度になることを紙製の三角形を使って実際に確認してください、という問題。

こういう紙の三角形を使います。


一番簡単なやり方：
三角形の角をちぎってこのように並べるとほら180度！確認終わり！


では、紙をやぶらないで確認するにはどうしたら良いでしょうか？

考えてみてください。

↓

↓

↓

↓

↓

↓

↓

↓

↓

↓

正解の解説です。

まず、どれか一つの角を反対側の辺に接するように折ります。
このとき、接する辺と折った線が平行になるようにします。


そうしたら後は両横の角を寄せるように折ります。
するとほら！三つの角で180度！ちぎらずに確認完了！


というわけで、みなさんも手を動かしてやってみると良いかと。
夏の終わりにレッツ算数！

ref.
- NHKオンライン | Ｅテレ ２３５５
http://www.nhk.or.jp/e2355/

追記120906:
「証明」と記述していたところをすべて「確認」に変更しました。
また、後半部分の証明を書いてみました。正確ではないかもしれませんが。

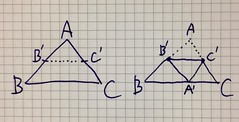
△ABCにおいて、辺ABの中点をB'、辺ACの中点をC'とする。
直線B'C'を軸に△AB'C'を角Aが辺BCに接するよう回転し、その接点をA'とする。
すると下記のことが言える。
(1) ∠B'A'B+∠B'A'C'+∠C'A'C=180
(2) ∠B'A'C'=∠BAC, ∠A'B'C'=∠ABC, ∠A'C'B'=∠ACB（三角形の相似）
(3) ∠B'A'B=∠A'B'C'=∠ABC, ∠C'A'C=∠AC'B'=∠ACB（錯角）
これらにより下記が導かれる。
∠ABC+∠BAC+∠ACB=180
よって三角形の内角の和は180度である。