【書評・感想】涙なしの統計学
2011-01-19-2
[BookReview]
先日読んだ小島本(「完全独習 統計学入門」[2011-01-16-1])に続いて統計のお勉強。
大学の統計学の講義の(確か)副読本だったこれ。
久しぶりに通読しました。
もう二十年近く前になるのか。
■D.ロウントリー / 涙なしの統計学

2001年に新版が出ていますね。
D.ロウントリー / 新・涙なしの統計学

確かに涙なしで読める「読み物」ですが、ポイントはしっかり押さえてあると思います。標本間の比較に重きがおかれています。二重盲検定で効果を確認するタスクがこの本の一つの目標かな。
以下、読書メモ:
傾向の尺度三つ:モード(mode)、メディアン(median)、平均(mean)
正規曲線のもとでの割合:
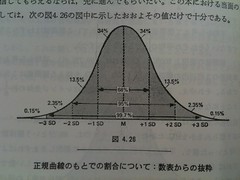
- M±1SD 2/3 68%
- 2SD(1.96) 95%
- 3SD 99.7%
- 2.5SD 99%
- SD一個分のレインジは全体の約1/6
z値 = (分布の平均-平均)/SD
統計量(Statistics)とパラメータ(Parameter)。前者は計れるもの、ローマ字表記。後者は正確に知ることができないもの、ギリシャ文字表記。
Sample と Population。
標本平均(Sample mean), S平均。
母集団平均(Population mean), P平均。
標準語差(Standard Error, SE) = 標本分布の標準偏差。
標本SDから母集団の平均を推測する話から入っている。小島本では母集団SDを使う話からだった。この本では標本数が十分にある状況を例に標本SDを使用。t分布の話(標本数が少ない)は後で出てくるが詳細は省かれている。
二重盲検定の話あり。標本間の比較。片側検定と両側検定。片側1%は2×1/3。
F検定、分散分析の話あり。基本的な考え方の解説。標本内分散と標本間分散。
相関と回帰。積率相関係数と順位相関係数があげられているがそれらの詳細説明はなく相関係数の標準誤差による検定の話。回帰直線の説明はあるが回帰式の作り方はなし。まあ「涙なし」なので。
大学の統計学の講義の(確か)副読本だったこれ。
久しぶりに通読しました。
もう二十年近く前になるのか。
■D.ロウントリー / 涙なしの統計学

2001年に新版が出ていますね。
D.ロウントリー / 新・涙なしの統計学

見慣れない記号や難解な数式に泣かされず、文章と図版による解説のみで統計学のエッセンスがマスターできるユニークな統計学への入門書。身近で親しみやすい具体例を基に、読者が自分の頭で考えることで理解していく解説のスタイルをとり、統計学の基本的な諸概念と実際の手法が自然に身に付くように工夫されている。初めて学ぶ人にとってのテキストであるとともに統計学に関心のあるすべての読者にとって含蓄のある「読み物」でもある。
確かに涙なしで読める「読み物」ですが、ポイントはしっかり押さえてあると思います。標本間の比較に重きがおかれています。二重盲検定で効果を確認するタスクがこの本の一つの目標かな。
以下、読書メモ:
傾向の尺度三つ:モード(mode)、メディアン(median)、平均(mean)
正規曲線のもとでの割合:

- M±1SD 2/3 68%
- 2SD(1.96) 95%
- 3SD 99.7%
- 2.5SD 99%
- SD一個分のレインジは全体の約1/6
z値 = (分布の平均-平均)/SD
統計量(Statistics)とパラメータ(Parameter)。前者は計れるもの、ローマ字表記。後者は正確に知ることができないもの、ギリシャ文字表記。
Sample と Population。
標本平均(Sample mean), S平均。
母集団平均(Population mean), P平均。
標準語差(Standard Error, SE) = 標本分布の標準偏差。
標本SDから母集団の平均を推測する話から入っている。小島本では母集団SDを使う話からだった。この本では標本数が十分にある状況を例に標本SDを使用。t分布の話(標本数が少ない)は後で出てくるが詳細は省かれている。
二重盲検定の話あり。標本間の比較。片側検定と両側検定。片側1%は2×1/3。
F検定、分散分析の話あり。基本的な考え方の解説。標本内分散と標本間分散。
相関と回帰。積率相関係数と順位相関係数があげられているがそれらの詳細説明はなく相関係数の標準誤差による検定の話。回帰直線の説明はあるが回帰式の作り方はなし。まあ「涙なし」なので。
この記事に言及しているこのブログ内の記事
