たつをの ChangeLog : 2005-01-23
線形時間で Suffix Array 作成
2005-01-23-1
[Algorithm]
週末自己啓発!アルゴリズムの勉強。趣味の世界。
taku-ku 氏に教えてもらった論文。線形時間で Suffix Array を作る話。
Suffix Tree 方式だと O(n) でできるのだがこれは違うやり方。
Juha K¨arkk¨ainen and Peter Sanders:
"Simple Linear Work Suffix Array Construction",
ICALP 2003, LNCS 2719, pp. 943-955, 2003.
<http://www.cs.helsinki.fi/u/tpkarkka/publications/icalp03.pdf>
Step 1: 3 で割り切れない位置(mod 3≠0)から始まる文字列のそれぞれの
先頭 3 文字(triple)にlexicographic namesを付与する。
これには基数ソートを使う。ソート後、先頭からlexicographic namesを
1,2,3,...と付与する。同じtripleには同じname。
もし、全てのtripleがユニークならばソートは完了。
そうでなければ、mod 3 = 1 の triple 列と mod 3 = 2 の triple 列を
連結した配列に対して、再帰的に Step 1 を行う。
Step 2: 3 で割り切れる位置(i: i mod 3 = 0)から始まるsuffixでsuffix
arrayを作る。ソートは最初の1文字 s[i] とそれに続く S_{i+1}
(s[i+1,i+2,...]) で行うのだが、 後者は Step 1 ですでにソートされて
るので楽々。
Step 3: 上記 2 つのsuffix arrayをマージして最終的なsuffix arrayを
作る。マージの際の文字列比較:
i(i mod 3 = 0), j(j mod 3 = 1) のときは、
s[i]+S_{i+1} と s[j]+S_{j+1} を比較するわけだが、
S_{i+1} と S_{j+1} は Step 2 ですでにソートされているので楽々。
i(i mod 3 = 0), j(j mod 3 = 2) のときは、
s[i]+s[i+1]+S_{i+2} と s[j]+s[i+1]+S_{j+2} を比較するので同じく楽々。
- なぜ、線形時間かというと、基数ソート(radix sort)が線形だから。
- 論文の後ろに C++ のサンプルコードがついている。
- テキストサイズのオーダーの配列をいくつか内部で使ってる。
メモリ使用効率に問題がありそう。
- つまり、実メモリを越えるサイズ(実際はそこまでいかなくても)の
テキストを対象にする場合、かなーり嬉しくないかも。
- lexicographic namesの付与がネック。
- 基数ソートはバケツデータ構造がいる。このあたりは実装レベルで
かなり時間がかかりそう。
- つか、日本語文字だとやばいんじゃない?
- 解説資料を発見:
東大の情報生命科学基礎・演習の資料「Suffix Trees and Arrays」
<http://www.hgc.jp/~tshibuya/classes/shibuya20040629.pdf>
- O(n) 時間で作る話があるといつも着目するのは「単語、行単位の
ソートはどうするか」という点。SUFARY だとよく使うので。
しかし、この手法を使うと文字単位以外では Step 2, 3 のうまみがな
い。単語や行のID化はしたくない。
- 結局、DNA配列には適すけど...といった感じか。
taku-ku 氏に教えてもらった論文。線形時間で Suffix Array を作る話。
Suffix Tree 方式だと O(n) でできるのだがこれは違うやり方。
Juha K¨arkk¨ainen and Peter Sanders:
"Simple Linear Work Suffix Array Construction",
ICALP 2003, LNCS 2719, pp. 943-955, 2003.
<http://www.cs.helsinki.fi/u/tpkarkka/publications/icalp03.pdf>
Abstract. [...]
1. recursively sort suffixes beginning at positions i mod 3 != 0.
2. sort the remaining suffixes using the information obtained in
step one.
3. merge the two sorted sequences obtained in steps one and two.
Step 1: 3 で割り切れない位置(mod 3≠0)から始まる文字列のそれぞれの
先頭 3 文字(triple)にlexicographic namesを付与する。
これには基数ソートを使う。ソート後、先頭からlexicographic namesを
1,2,3,...と付与する。同じtripleには同じname。
もし、全てのtripleがユニークならばソートは完了。
そうでなければ、mod 3 = 1 の triple 列と mod 3 = 2 の triple 列を
連結した配列に対して、再帰的に Step 1 を行う。
Step 2: 3 で割り切れる位置(i: i mod 3 = 0)から始まるsuffixでsuffix
arrayを作る。ソートは最初の1文字 s[i] とそれに続く S_{i+1}
(s[i+1,i+2,...]) で行うのだが、 後者は Step 1 ですでにソートされて
るので楽々。
Step 3: 上記 2 つのsuffix arrayをマージして最終的なsuffix arrayを
作る。マージの際の文字列比較:
i(i mod 3 = 0), j(j mod 3 = 1) のときは、
s[i]+S_{i+1} と s[j]+S_{j+1} を比較するわけだが、
S_{i+1} と S_{j+1} は Step 2 ですでにソートされているので楽々。
i(i mod 3 = 0), j(j mod 3 = 2) のときは、
s[i]+s[i+1]+S_{i+2} と s[j]+s[i+1]+S_{j+2} を比較するので同じく楽々。
- なぜ、線形時間かというと、基数ソート(radix sort)が線形だから。
- 論文の後ろに C++ のサンプルコードがついている。
- テキストサイズのオーダーの配列をいくつか内部で使ってる。
メモリ使用効率に問題がありそう。
- つまり、実メモリを越えるサイズ(実際はそこまでいかなくても)の
テキストを対象にする場合、かなーり嬉しくないかも。
- lexicographic namesの付与がネック。
- 基数ソートはバケツデータ構造がいる。このあたりは実装レベルで
かなり時間がかかりそう。
- つか、日本語文字だとやばいんじゃない?
- 解説資料を発見:
東大の情報生命科学基礎・演習の資料「Suffix Trees and Arrays」
<http://www.hgc.jp/~tshibuya/classes/shibuya20040629.pdf>
- O(n) 時間で作る話があるといつも着目するのは「単語、行単位の
ソートはどうするか」という点。SUFARY だとよく使うので。
しかし、この手法を使うと文字単位以外では Step 2, 3 のうまみがな
い。単語や行のID化はしたくない。
- 結局、DNA配列には適すけど...といった感じか。
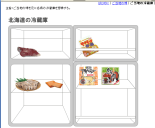
借力[CHAKURIKI] 県民の噂 - ご当地の冷蔵庫
<http://www.chakuriki.net/karuta/#03>
こういうアフィリエイト商品提示方法(アサマシ方法)があったか。
「気になる棚」<http://nais.to/attic/kininarutana/> より断然筋が良い。
「食器棚」とか作ってみるか?
<http://www.chakuriki.net/karuta/#03>

主旨:ご当地の噂を元に各県の冷蔵庫を想像する。そうか!冷蔵庫か!
こういうアフィリエイト商品提示方法(アサマシ方法)があったか。
「気になる棚」<http://nais.to/attic/kininarutana/> より断然筋が良い。
「食器棚」とか作ってみるか?
iPod mini 来ました!
2005-01-23-3
[Gadget]
今朝、届きました。 ref. [2005-01-21-6]
■Apple iPod mini 4GB (ブルー) M9436J/A

ちょっとトラブル。自宅PCは、USB1.1 なので USB2.0 経由で使えないことは
分かっていて、IEEE1394 (Firewire) で使おうと計画していたのですが、
付属のFirewire接続コードは6ピンでした(PC本体は4ピン仕様)。
おでかけついでに 6ピン→4ピン変換アダプタを買ってきました。
(ELECOM IEEE1394 変換コネクタ AD-IE6FT4M)
4ピンFirewireだと充電できないんだけど、当面はそれでいいです。
USB2、やはりないと他でも不便なので、PCカードなどで使えるようにする
予定。
■Apple iPod mini 4GB (ブルー) M9436J/A

ちょっとトラブル。自宅PCは、USB1.1 なので USB2.0 経由で使えないことは
分かっていて、IEEE1394 (Firewire) で使おうと計画していたのですが、
付属のFirewire接続コードは6ピンでした(PC本体は4ピン仕様)。
おでかけついでに 6ピン→4ピン変換アダプタを買ってきました。
(ELECOM IEEE1394 変換コネクタ AD-IE6FT4M)
4ピンFirewireだと充電できないんだけど、当面はそれでいいです。
USB2、やはりないと他でも不便なので、PCカードなどで使えるようにする
予定。
ロフ地下
2005-01-23-4
[Stationery]
ちょっと前から渋谷のロフトの地下が文房具売り場になりました。
東急ハンズの文具売場よりもよいかと。今日は時間がなかったのもあるけど、ハンズには行かず。ちびポストイットもあるし、とりあえずロフ地下に行っとけばいいや的。
ref. [2004-12-11-1]

ちなみに同じフロアに無印良品もあります。
東急ハンズの文具売場よりもよいかと。今日は時間がなかったのもあるけど、ハンズには行かず。ちびポストイットもあるし、とりあえずロフ地下に行っとけばいいや的。
ref. [2004-12-11-1]

ちなみに同じフロアに無印良品もあります。
都内某所で読書会。第7回。
■サイモン シン / 暗号解読-ロゼッタストーンから量子暗号まで

古典的な暗号から、ヴィジュネル暗号、エニグマ、公開鍵、量子暗号まで。
暗号だけでなく、古代文字の解読も。はっきり言って面白すぎる。説明も分かりやすい。歴史読み物好きな方もどうぞ。
- エニグマの解読がちょっとよく分からなかった。チューリングの3台つなげるやつ。しかし、読書会での議論により理解できた。乱暴に言ってしまえば、文字列マッチアルゴリズムみたいな感じかと。
- ヒエログリフや線文字Bの話を読んでると、パラダイムシフト時のアカデミック界の対応というものについて考えさせられるな。
- 量子暗号は分かった気になれる!今まで読んだ説明で一番分かりやすい。
ただの読み物とみせかけて、実は暗号技術の概要を学べる良書なのです。
ざっと読んでも分かった気になれるし、じっくり読めばしっかり分かる。
おすすめです。
■サイモン シン / 暗号解読-ロゼッタストーンから量子暗号まで

古典的な暗号から、ヴィジュネル暗号、エニグマ、公開鍵、量子暗号まで。
暗号だけでなく、古代文字の解読も。はっきり言って面白すぎる。説明も分かりやすい。歴史読み物好きな方もどうぞ。
- エニグマの解読がちょっとよく分からなかった。チューリングの3台つなげるやつ。しかし、読書会での議論により理解できた。乱暴に言ってしまえば、文字列マッチアルゴリズムみたいな感じかと。
- ヒエログリフや線文字Bの話を読んでると、パラダイムシフト時のアカデミック界の対応というものについて考えさせられるな。
- 量子暗号は分かった気になれる!今まで読んだ説明で一番分かりやすい。
ただの読み物とみせかけて、実は暗号技術の概要を学べる良書なのです。
ざっと読んでも分かった気になれるし、じっくり読めばしっかり分かる。
おすすめです。
この記事に言及しているこのブログ内の記事
- 「たつをの ChangeLog」で人気のアマゾン商品ランキング 2007 (2008-02-25)
- 超オススメ本「暗号解読」が文庫化 (2007-07-05)
- おすすめガイドブック「コンピュータの名著・古典100冊」 (2007-04-15)
- 「ビッグバン宇宙論」は読むべし (2006-10-11)
- 2005年の10冊 (2006-02-26)
- 新春ポッドキャスト対談「ツイてる!ポッドキャスト2006」(1) (2006-01-01)
- 読書会で「フェルマーの最終定理」 (2005-10-30)
- ソーシャルブックマークで暗号化コメントが流行るか (2005-06-24)
- モンテ・クリスト伯、読んでます (2005-02-04)
- 2005 年 1 月に読んだ本 (2005-01-31)
たつをの ChangeLog
Powered by chalow